Pi Squared: The Next Generation of Verifiable Computing

How Pi Squared’s Universal Settlement Layer will unify the fractured Web3 space.

Grigore Roșu
Founder & CEO at Pi Squared
Professor, University of Illinois Urbana Champaign

Verifiable computing is emerging as the future of computing. It is the only scientific method known that promises correct results for computations done in completely untrusted remote computing environments, which is particularly important for decentralized Web3 infrastructure. Unfortunately, state-of-the-art verifiable computing solutions suffer from a series of technological limitations that reduce their applicability or our trust in them:

• They are specific to a particular computing model, e.g. a programming language (PL), a virtual machine (VM), an instruction set architecture (ISA), or even a program or algorithm;
• They require translations from one language to another, e.g. compilers, known to have errors unless they are formally verified, which is very expensive and thus usually not done in practice; 
• They are not provably correct, so their results can be and sometimes are indeed wrong — unless they are formally verified, which is an even harder problem than formally verifying compilers; and finally, 
• They are excruciatingly slow.

Pi Squared proposes a major overhaul of the verifiable computing field, which we refer to as Verifiable Computing 2.0. Instead of relying on adhoc solutions and languages, Pi Squared builds upon one of the oldest and most well-established fields in computer science, formal semantics, which is the only scientific method known that allows us to rigorously reason about programs and computations. Specifically, formal semantics of a particular computing model, e.g. a PL, a VM, an ISA or even a particular program or algorithm, is a mathematical theory in a mathematical logic, which allows us to mechanically reduce any computation in that model to a rigorous mathematical proof. This allows us to shift focus from proving adhoc computations in adhoc languages to uniformly proving the integrity of mathematical proofs cryptographically, which is a simpler yet more general problem than proving computing.

The Core Innovation: Proof of Proof

There are many semantic frameworks developed by the computer science and mathematics community over the last decades. All of them allow us to define formal semantics and reduce computation to mathematical proofs. We prefer to use the K Framework in Pi Squared, which was invented in 2003 by the Formal Systems Laboratory at the University of Illinois at Urbana-Champaign (UIUC). It has been advanced and improved ever since by Runtime Verification as well as by an international community of students, researchers and enthusiasts.

The picture below illustrates how K works at a high level:

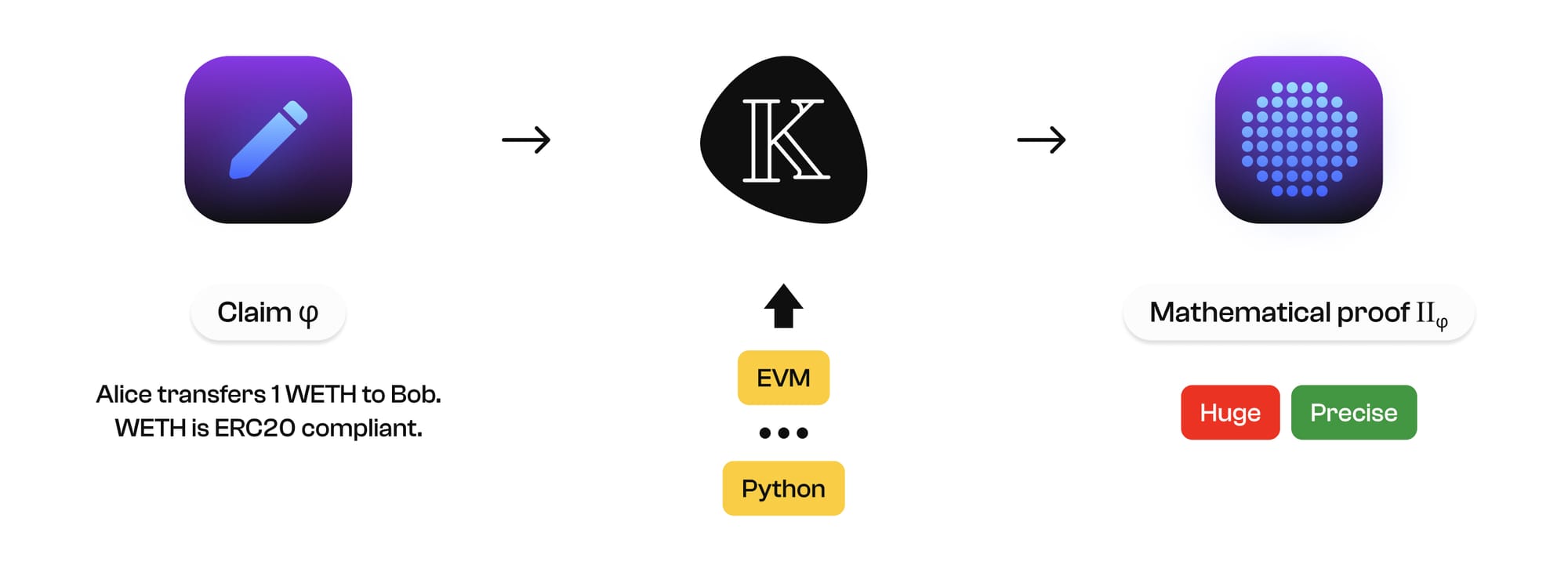
First, K takes as input a formal semantics (yellow box in the picture) as a mathematical theory, which usually defines a particular computational model, such as a programming language like Python or a virtual machine like an EVM (a good example is the K EVM semantics at https://jellopaper.org/), as well as a claim made about that semantics, such as a particular program on a particular input generates a particular output. K then constructs a rigorous mathematical proof of the claim, attesting to the mathematical correctness of the claim. Internally, K generates specialized interpreters and proof automation triggered by them, but ultimately what matters is the generated mathematical proof, which can be checked independently of K and its internal tools. This is done using mathematical proof checkers, which check the integrity of the mathematical proof independently of how the proof was produced. Anybody and anything can generate the mathematical proof, even ChatGPT, provided that the proof checks as correct. However, anecdotal evidence in the formal semantics community tells us that it is a non-trivial engineering challenge to actually produce such rigorous and complete mathematical proofs. Indeed, it took K more than 20 years of community development to get there.

In theory, we could use such mathematical proofs as ultimate correctness certificates of computational claims. In practice, such mathematical proofs tend to be huge, because they go all the way down to the axioms defining the language and the proof rules of mathematical reasoning, so it is rather impractical to send them across a network in order to be checked. The second major component of Pi Squared is a zero-knowledge (ZK) cryptographic circuit that implements a checker for the integrity of mathematical proofs:

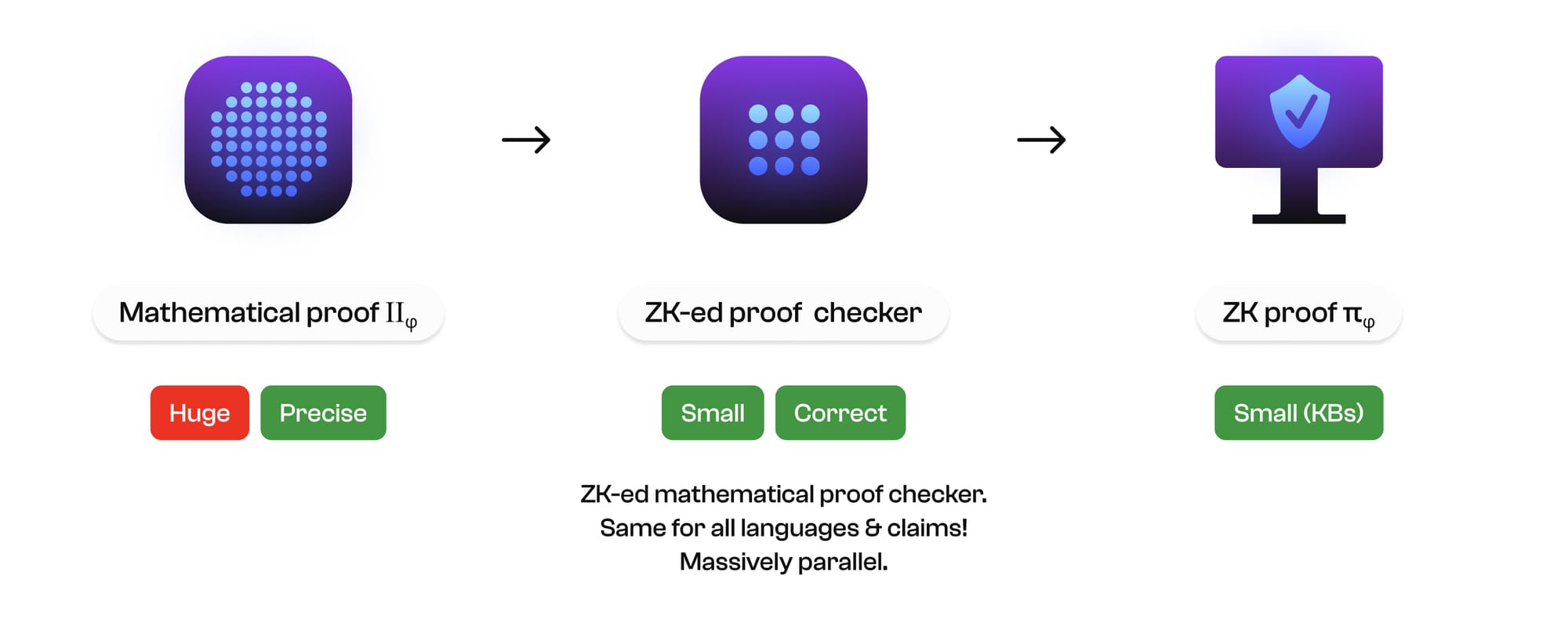
The ZK-ed mathematical checker yields a succinct cryptographic argument that a mathematical proof of the claim was presented to it as input and checked, which therefore acts as a small certificate, or ZK proof, that attests with a very high probability that the claim is indeed correct. The creation of a (ZK) proof of a (mathematical) proof is the inspiration for our name, Pi Squared (𝝿²).

The community recognizes that there is no silver-bullet PL, VM, or ISA, and there never will be. Any robust PL or VM worth its salt is continuously updated, with new versions released every few months. Keeping up with these changes is a significant challenge on its own. End-to-end, Pi Squared achieves the same overall result as the existing verifiable computing approaches, but instead uses a general and universal pipeline that works with all PLs and VMs alike, without a need for compilers and/or translators. Its trust base is minimal, consisting of only the formal semantics of the language, which is unavoidable in any approach that claims correctness, and a small cryptographic circuit for checking the integrity of mathematical logic proofs. There is nothing specific to any particular programming language or virtual machine that requires to be formally verified, that is, Pi Squared yields universal and correct by construction verifiable computing.

Uniting Web3: The Universal Settlement Layer

Web3 is plagued by fragmentation of both liquidity and attention. There are now countless unique blockchains, often with unique programming languages or virtual machines, that users and developers must choose from. Through its language universality and correctness by construction, Pi Squared offers a unique opportunity to unify these siloed ecosystems for both users and developers, in a trust-minimized manner. We are accomplishing this unification by creating a Universal Settlement Layer (USL) that can be used to settle transactions and contract interactions between disparate blockchains using different programming and/or virtual machine languages. The languages themselves are settled on the USL, through their formal semantics: 

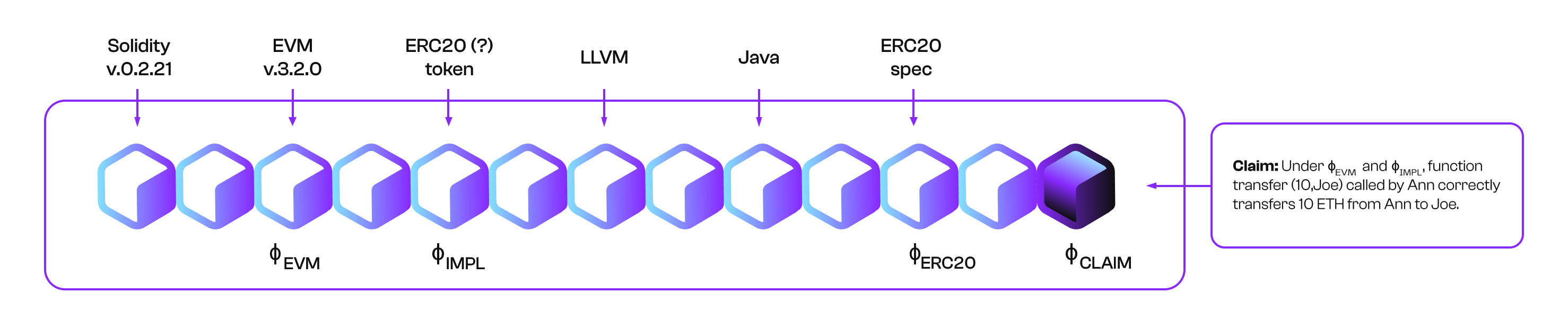
While our primary goal at Pi Squared is to revolutionize verifiable computing, the USL’s short-term goal is to empower developers to build interoperable smart contracts across any blockchain VMs or languages. Longer-term, the USL’s goal is to embrace Pi Squared’s generality to prove any mathematical truth, not only computations, and thus provide us and future generations with the ideal infrastructure to settle the entirety of science and knowledge. Indeed, there is no fundamental difference between EVM and Euclidean Geometry in Pi Squared, they are both mathematical theories defined axiomatically, and no difference between “Alice transfers one ERC20 token to Bob” and “Pythagoras theorem”, they are both mathematically provable claims.

By using the USL, developers will be able to build applications that span any blockchain. Layer-1s and Layer-2s will become more universal and efficient, and users will be able to avoid traditional bridging risks. Because the USL can settle any computational claims, it also creates a way for remote computing provided by centralized companies like Amazon or Google to become trustless and verifiable without the excessive costs associated with existing settlement layers. At Pi Squared, we envision the USL first being used to assist crypto applications that are either inherently multi-chain in nature or would benefit from being multi-chain, and crypto ecosystems (Layer-1s and Layer-2s) that are suffering from fragmentation. However, the concept of Proof of Proof and the USL both offer lots of potential for developers to use them in new and unique ways. It’s impossible to predict all the ways in which dApp builders can use the technology in imaginative ways to improve and expand the reach of their applications.

To learn more about Pi Squared, the idea of “Proof of Proof,” and the USL, check out this presentation, along with the whitepaper as well as Pi Squared’s Documentation.